| Vocab Bar | |
|---|---|
| Recursion | Recursion is a programming technique in which a method calls itself in order to accomplish a goal. |
| Termination Condition | The condition that causes the method to end. |
Recursion is a very popular programming technique that can be used to solve large/complex problems. A recursive method has two key elements:
-
A recursive method calls itself (sometimes multiple times, depending on the scenario).
-
A recursive method has a termination condition (or multiple, depending on the scenario).
For example, let’s say you wanted to print the factorial of a number (which is the product of an integer and all the positive integers below it). The iterative implementation (using a for loop) for this problem would look like this:
public static int factorialIterative(int n) {
int value = 1;
for (int i = n; i > 0; i--) {
value *= i;
}
}
Now, the recursive implementation for this problem would look like this:
public static int factorial(int n) {
// termination condition
if (n == 0) {
return 1;
}
// re-calls method
return n * factorial(n-1);
}
The above two statements output the same value. What happens if we make the method call factorial(5) (the recursive method)? Let’s walk through it step by step.
| Value of n | Return statement |
|---|---|
5 |
return 5 * factorial(4) |
4 |
return 4 * factorial(3) |
3 |
return 3 * factorial(2) |
2 |
return 2 * factorial(1) |
1 |
return 1 * factorial(0) |
0 |
return 1 |
The above table still has lots of method calls, which means it is not fully simplified. Here is a simplification of the table:
| Value of n | Return statement |
|---|---|
5 |
return 5 * 4 * 3 * 2 * 1 * 1 |
4 |
return 4 * 3 * 2 * 1 * 1 |
3 |
return 3 * 2 * 1 * 1 |
2 |
return 2 * 1 * 1 |
1 |
return 1 * 1 |
0 |
return 1 |
Finally, let’s simplify one more time:
| Value of n | Return statement |
|---|---|
5 |
return 120 |
4 |
return 24 |
3 |
return 6 |
2 |
return 2 |
1 |
return 1 |
0 |
return 1 |
Based on the above table, factorial(5) returns 120. The reason the method did not continue calling itself was the termination condition, which returned 1 when n == 0. The termination condition is crucial to recursion – without the termination condition, the code results in an infinite loop.
One important usage of recursion is recursive backtracking – when you continue to try solutions until you reach an issue, at which point you return to a simpler solution and continue the program. For example, let’s say you wanted to test if a maze was solvable. A program could test multiple routes through the maze, and determine whether or not the maze had a solution. A maze-solving recursive method would contain the following parts:
-
A termination condition to see if the end of the maze has been reached.
-
Multiple if statements, each containing a recursive call checking whether the next space is open. (You check whether you can move up, down, left, or right.) If true, return true (thus the method returns a boolean).
-
A “flag” that marks the positions that you visited with a special icon so you don’t revisit a path twice.
-
A backtrack statement at the end of the method that allows you to backtrack from a dead-end path (shown in below gif).
-
Multiple parameters to keep track of the current x position, the current y position, and the current maze.
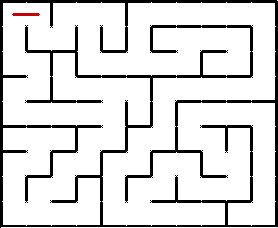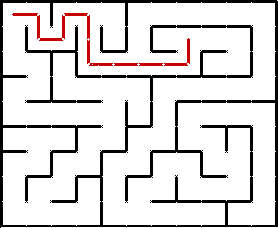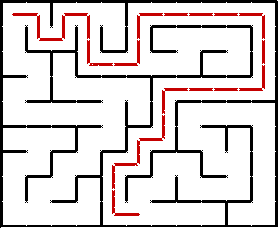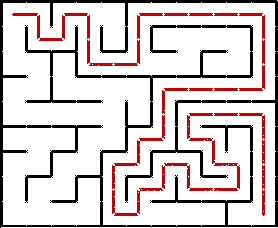
A program solving a maze recursively. Source
Although recursion is often difficult to understand at first, with enough practice, you can master this useful technique.
Lesson Quiz
1. What happens if a recursive method doesn’t have a termination condition?
2. Is it possible for a recursive method to have multiple termination conditions?
Written by Chris Elliott
Notice any mistakes? Please email us at learn@teamscode.com so that we can fix any inaccuracies.